「40-32÷2」等於什麼?!正確答案是4!真的沒騙你們!
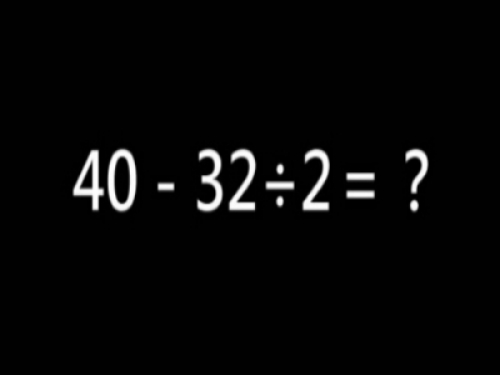
你們能夠回答「40-32÷2=?」是多少嗎?
小學生一定會開心地回答,是「4!」。
接着我們線上找到文科和理科的學生和社會人士,
詢問他們答得對不對。
文科的大哥哥大姊姊們,有些人微笑以對,沒有說話;
有的則直接曖昧的笑一笑,說道:「人家是文科生,所以不知道呢~」
這些文科生都覺得這問題必定有鬼,但又不曉得問題在哪裡,
只好採迂迴態度,拒絕回答問題。
理科生的大哥哥大姊姊則點頭,讚許說道:
「小學生解出來?真不錯,答案就是『4!』沒錯。」
「什麼!答案不是應該24嗎?先乘除後加減,32÷2等於16後,再讓40減去,不就應該這樣嗎?」
答案24一點也沒錯,所以4!也是正確答案。
「!」表示一個正整數的階乘,是指所有小於及等於該數的正整數的積。
所以--
「40-32÷2=?」,正確答案是4!
喔,沒騙你們!
4!(4的階乘)。
4! = 4×3×2×1 = 24
答案:
40-32÷2=4!
各位懂了嗎?懂的話,那就下課。
「40-32÷2=?」,正確答案是4!
沒想到答案的真相竟是這樣!
階乘是基斯頓‧卡曼(Christian Kramp,1760~1826)於 1808 年發明的運算符號,是數學術語。
一個正整數的階乘(英語:factorial)是所有小於及等於該數的正整數的積,並且0的階乘為1。
自然數n的階乘寫作n!。
1808年,基斯頓‧卡曼引進這個表示法。
亦即n!=1×2×3×...×n。
階乘亦可以遞歸方式定義:0!=1,n!=(n-1)!×n。
正整數階乘指從 1 乘以 2 乘以 3 乘以 4 一直乘到所要求的數。
例如所要求的數是 4,則階乘式是 1×2×3×4,得到的積是 24,24 就是 4 的階乘。
例如所要求的數是 6,則階乘式是 1×2×3×……×6,得到的積是 720,720 就是 6 的階乘。
例如所要求的數是 n,則階乘式是 1×2×3×……×n,設得到的積是 x,x 就是 n 的階乘。







